mark一下一个online的编译环境: https://code.labstack.com
HCI command笔记
规范 Vol2 的Part E,讲HCI command的第7章有几个command,看起来很有用,这里list下
7.5.1 Read Faild Contact Counter command

这个计数器(Failed_Contact_Counter,两个字节)是用来记录由于flush timeout到期(一般是因为空气中信号干扰比较多,数据包重传比较多)而flush掉的数据包的个数,在做bt music的时候经常看到smartphone送过来的数据包的序列号不连续,如果smartphone有用这个command来monitor数据包的状况的话,就比较容易看到这个现象。
When the 802.11 PAL receives an HCI_Read_Failed_Contact_Counter command it shall return the number of consecutive incidents in which the remote device didn’t respond after the flus>h timeout had expired, and the L2CAP packet that was currently being transmitted was automatically flushed. The Failed Contact Counter is specific to each logical link.
7.1.47 Truncated Page command

可以用来探测目标设备在不在可连接范围内?
The HCI_Truncated_Page command is used to page the BR/EDR Controller with the specified BD_ADDR and then abort the paging sequence after an ID response has been received. See [Vol >2] Part B, Section 8.3.3 for additional information.
复习下page的几个步骤,请看下面的两张图:
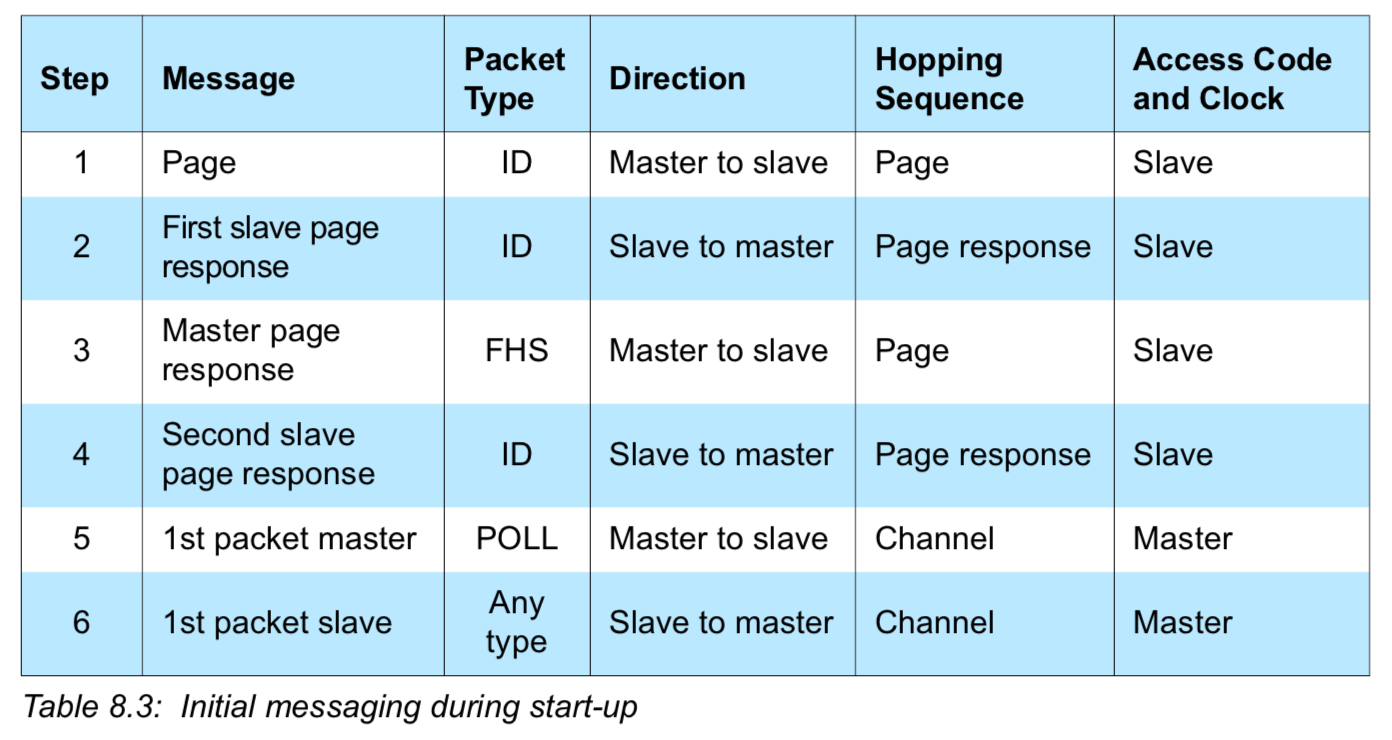
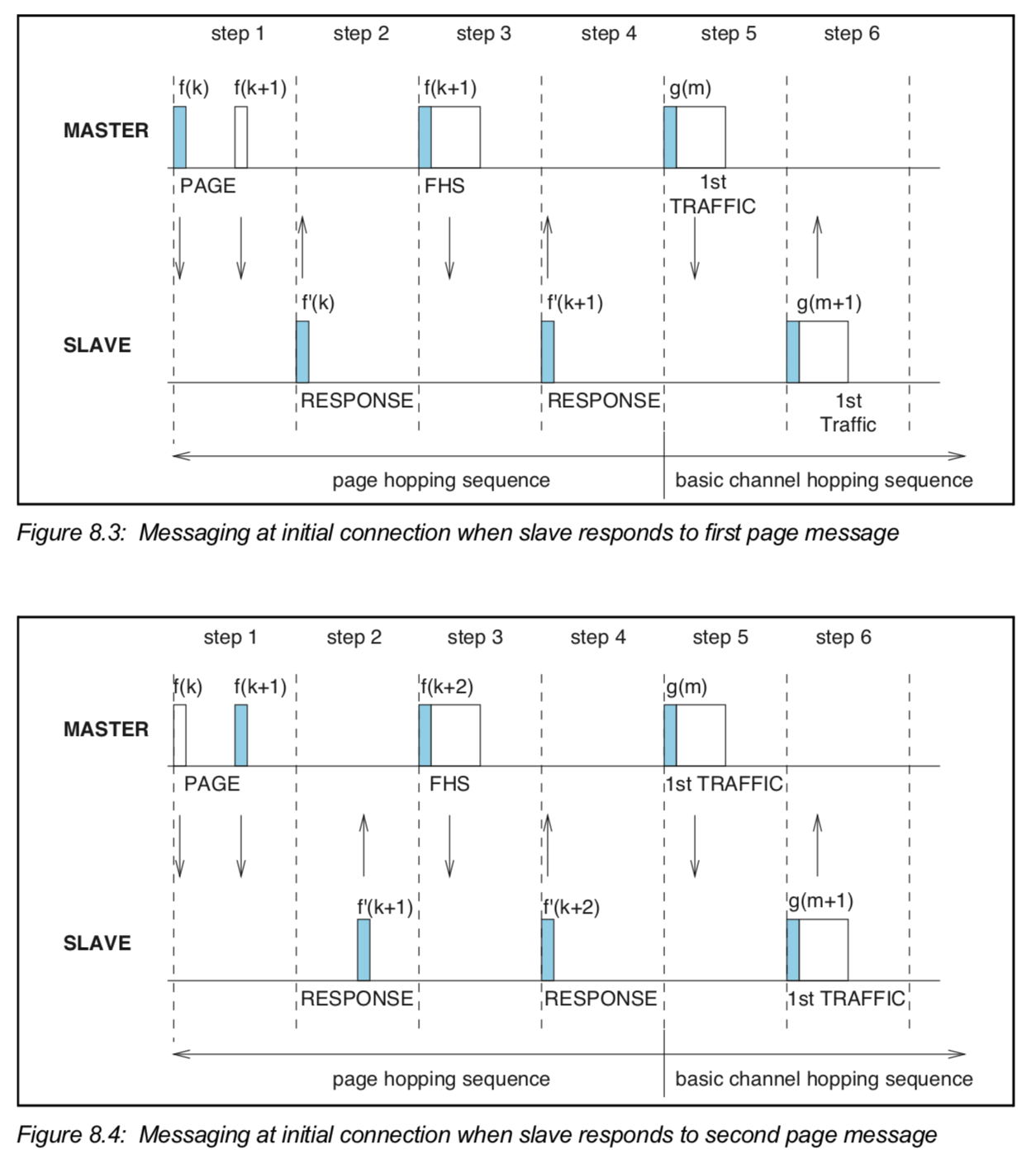
BLUETOOTH CORE SPECIFICATION Version 5.1 | Vol 2, Part E page 1112
hexo 中启用数学公式
本文来自 https://blog.csdn.net/crazy_scott/article/details/79293576 感谢原作者。
安装插件
- 首先我们需要安装Mathjax插件
npm install hexo-math —save
2 更换Hexo的markdown渲染引擎,hexo-renderer-kramed引擎是在默认的渲染引擎hexo-renderer-marked的基础上修改了一些bug,两者比较接近,也比较轻量级。
npm uninstall hexo-renderer-marked —save
npm install hexo-renderer-kramed —save
解决语义冲突
由于LaTeX与markdown语法有语义冲突,在markdown中,斜体和加粗可以用或者_表示,在这里我们修改变量,将_用于LaTeX,而使用表示markdown中的斜体和加粗。
在博客根目录下,进入node_modules\kramed\lib\rules\inline.js,把第11行的escape变量的值做相应的修改:
//escape: /^\([\`{}[]()#$+-.!_>])/,
escape: /^\([`[]()#$+-.!_>])/,
这一步是在原基础上取消了对,{,}的转义(escape)。
同时把第20行的em变量也要做相应的修改:
// em: /^\b_((?:__|[\s\S])+?)_\b|^*((?:**|[\s\S])+?)*(?!*)/,
em: /^*((?:**|[\s\S])+?)*(?!*)/,
更改配置文件
这里是最重要的一步,我找了好久才在这个网站中找到适用的解决办法。
进入到主题目录,找到_config.yml配置问题,把mathjax默认的false修改为true,并更换cdn的url,具体如下:
# MathJax Support
mathjax:
enable: true
per_page: true
#cdn: //cdn.bootcss.com/mathjax/2.7.1/latest.js?config=TeX-AMS-MML_HTMLorMML
cdn: //cdnjs.cloudflare.com/ajax/libs/mathjax/2.7.1/MathJax.js?config=TeX-AMS-MML_HTMLorMML
如果配置文件里已经有这一行而且版本比这行还新的话,就可以不用更新。
写博客
在每次需要用LaTeX渲染的博文中,在文章的Front-matter里启动mathjax,具体如下:
-—
title: Hexo Usage
date: 2018-2-8 21:01:30
tags: Hexo
mathjax: true
-—
TRNG
TRNG(True Random Number Generator)是真随机数生成器。
真随机数生成器通常是通过放大电路的热噪声来产生随机数,温度高于绝对零度的原子都存在热运动,在集成电路里这些原子的热运动会在电路里产生噪声,噪声会使得电路中的电压存在微小的起伏,TRNG就是通过放大这些微小的起伏来产生随机数。
不过TRNG也有不少缺点。
- 首先就是产生随机数的速度很低,因为噪声放大电路有低通特性,使得高频的噪声被滤除了,而放大低频噪声就需要较长的时间,使得TRNG的工作频率受限。
- 其次是电路系统里有很多不同的噪声,但并不是所有噪声都是随机的,比如电源噪声中很大一部分就是和系统时钟强相关的。而TRNG是一个放大极小信号的电路,它对外界干扰是极其敏感的,为了避免外界非随机信号的干扰TRNG必须要耗费不少功率和面积在屏蔽上。由于面积和功耗限制,CPU中不能内置很多个TRNG;由于频率限制,单个TRNG输出的随机数数量有限,这使得单靠TRNG产生的随机数数量不足以满足系统需要。
还有用其他方法来生成随机数的,比如有个网站专门提供生成随机数的服务Random,该网站的随机数来自大气噪声(atmospheric noise)。
关于真随机数和伪随机数
伽罗华域
伽罗华(法国,1811~1832)才华横溢,可惜在21岁时早早死于情场决斗。他证明了:对于给定的一个素数次不可约方程能判断出它是否能根式求解。
Bluetooth在bit streaming过程中计算Sync word,HEC,FEC及data whitening时使用到了伽罗华域中的计算规则来处理比特流,本文就收集到的信息做个总结。
一个元素个数有限的域称为有限域,或者伽罗华域(Galoisfield)
- 有限域中元素的个数为一个素数,记为GF(p),其中p为素数;
一个大于1的整数,如果它的正因数只有1和它本身,就叫做素数,否则就叫做合数
有限域中运算满足
– 交换律:a+b = b+a, a·b = b·a
– 结合律:(a+b)+c = a+(b+c), a·(b·c) = (a·b)·c
– 和分配律:a·(b+c) = a·b+a·c将GF(p)延伸为一个含有$p^m$个元素的域,称为GF(p)的扩展域,表示为GF($p^m$),m是一个非零正整数。
注意:GF(p)是GF($p^m$)的子集。
二进制域GF(2)是扩展域GF($2^m$)的一个子域,类似于实数域是复数域的一个子域一样。除了数字0和1之外,在扩展域中还有特殊的元素,用一个新的符号a表示。GF($2^m$)中任何非0元素都可由a的幂次表示。
有限元素的集合GF($2^m$),只能含有$2^m$个元素,并且对乘法封闭,其约束条件为$a^{(2^m−1)}$+1=0
• 根据这个多项式限制条件,任何幂次等于或超过$2^m-1$的域元素都可降阶为下述幂次小于$2^m-1$的元素:
这样,GF($2^m$)的元素可表示为:
扩展域$GF(2^m)$中的加法
• 在$GF(2^m)$中,将每个非0域元素用多项式$a_i(x)$表示,其系数至少有一个不为0。对于i=0,1, 2,…,$2^m-2$,有:
• 先看m=3,有限域表示为$GF(2^3)$,下表为上式描述的基本元素(Primitive Element) ${x^0,x^1,x^2}$映射为7个元素{$a_i$}和一个0元素。表中的各行是二进制数字序列,代表上式中的系数$a_{i,0}、a_{i,1}、a_{i,2}$的取值。
| _ | $x^0$ | $x^1$ | $x^2$ |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| $a^0$ | 1 | 0 | 0 |
| $a^1$ | 0 | 1 | 0 |
| $a^2$ | 0 | 0 | 1 |
| $a^3$ | 1 | 1 | 0 |
| $a^4$ | 0 | 1 | 1 |
| $a^5$ | 1 | 1 | 1 |
| $a^6$ | 1 | 0 | 1 |
| $a^7$ | 1 | 0 | 0 |
多项式$f(x)=1+x+x^3$ 为GF($2^3$)的元素与基本元素之间的映射。
有限域中两个元素的加法定义为两个多项式中同幂次项系数 进行模2加,即
$a^i+a^j=(a_{i,0}+a_{j,0}) + (a_{i,1}+a_{j,1})x + … + (a_{i,m-1}+a_{j,m-1})x^{m-1}$
• 有限域的本原多项式。本原多项式定义了域GF($2^m$), 一个多项式是本原多项式的充要条件:
一个m阶的不可约多项 式f(x),如果f(x)整除$x^n+1$的最小正整数n满足$n=2^m-1$,则该多项式是本原的。
关于多项式在伽罗华域的求根
以$p(x) = 1 + x + x^3$ 为例,多项式的幂次为m=3,所以由p(x)所定义的域中包含了$2^m=2^3=8$个元素。求解p(x)的根就是指找到x 使p(x)=0。由高斯的基本代数学理论我们知道,对于幂次为m的多项式必然有m个根。对于这个例子,p(x)=0有3个根,由于这3个根不可能位于与p(x)系数相同的有限域中,而是位于扩展域GF($2^3$)中。
用扩展域的元素 a来定义多项式p(x)的根,可写成如下形式:p(a)=0
即 $1+a+a^3=0$,在该多项式两边都加上 1 + a, 就可以得到$a^3=1+a$ 这意味着$a^3$可以表示为更低阶a项的加权和。
类似地有:
$a^4$=a$a^3$=a(1+a)=a+$a^2$
$a^5$=a$a^4$=a(a+$a^2$)=$a^2$+$a^3$=1+a+$a^2$
$a^6$=a$a^5$=a(1+a+$a^2$)=a+$a^2$+$a^3$=1+$a^2$
$a^7$=a$a^6$=a(1+$a^2$)=a+$a^3$=1=$a^0$
所以,有限域GF($2^3$)的8个元素为 ${0,a^0,a^1,a^2,a^3,a^4,a^5,a^6}$
这8个元素中哪些是p(x)=0的3个根呢?我们可通过枚举 找到!
p($a^0$)=1, $a^0$不是
p($a^1$)=1+a+$a^3$=0, $a^1$是
p($a^2$)=1+$a^2$+$a^6$=1+$a^0$=0, $a^2$是
p($a^3$)=1+$a^3$+$a^9$=1+$a^3$+$a^2$=1+$a^5$=$a^4$, $a^3$不是
p($a^4$)=1+$a^4$+$a^12$=1+$a^4$+$a^5$=1+$a^0$=0, $a^4$是
同理可计算p($a^5$)、p($a^6$)都不等于0,所以p(x)=1+x+$x^3$的 3个根是a, $a^2$, $a^4$
主要参考文献有
FEC的介绍
存在主义咖啡馆
- 如果你和你想做的事情不在同一个频道,你就会浪费很多精力。等你有机会做你想做的事情的时候,你可能已经没有力气或时间了。
- 每一天都有很多人想要让你把你的时间和精力花在他们身上。比如你收到的邮件。如果你打算参加所有活动,参与每次促销,享用每一顿不请自来的服务,你就没有空闲时间了。这还只是邮件而已。再想想那些想通过电视、网络、餐厅、旅游地等等来吸引你注意力的人。你很快就发现,自己在做大家都在做的事,或者别人想让你做的事。
- 为什么人们把那么多时间花在准备工作上,而不是直接去做自己想做的事。部分原因就在于我们每天暴露在大量营销信息中,如果不谨慎点儿,我们肯定会把自己的幸福和满足寄托在某样产品或是服务上。最后我们会陷入财务困境,必须不断去做事情去挣钱,尽管那些事情不是我们真正想做的。
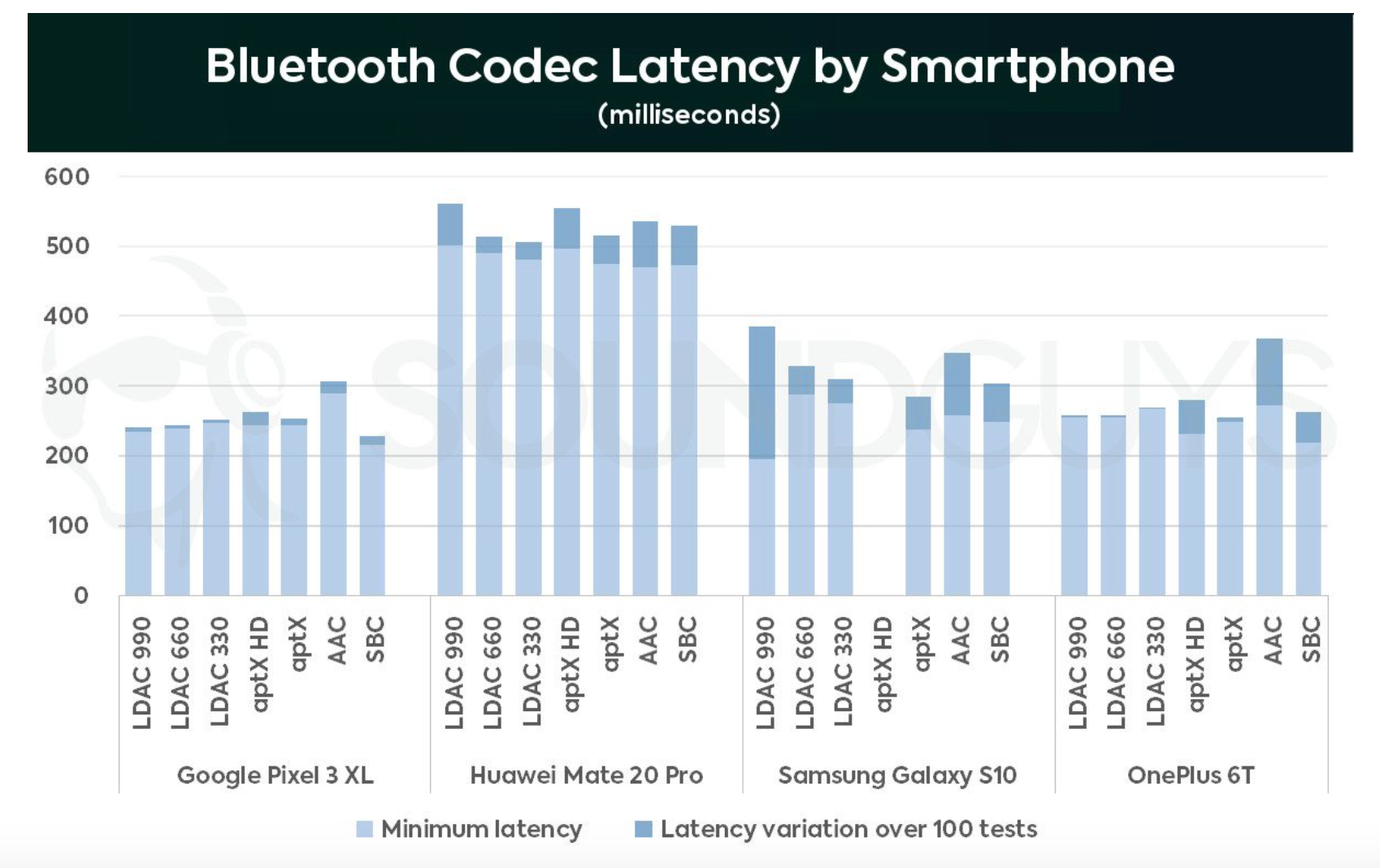
BT Codec 总结
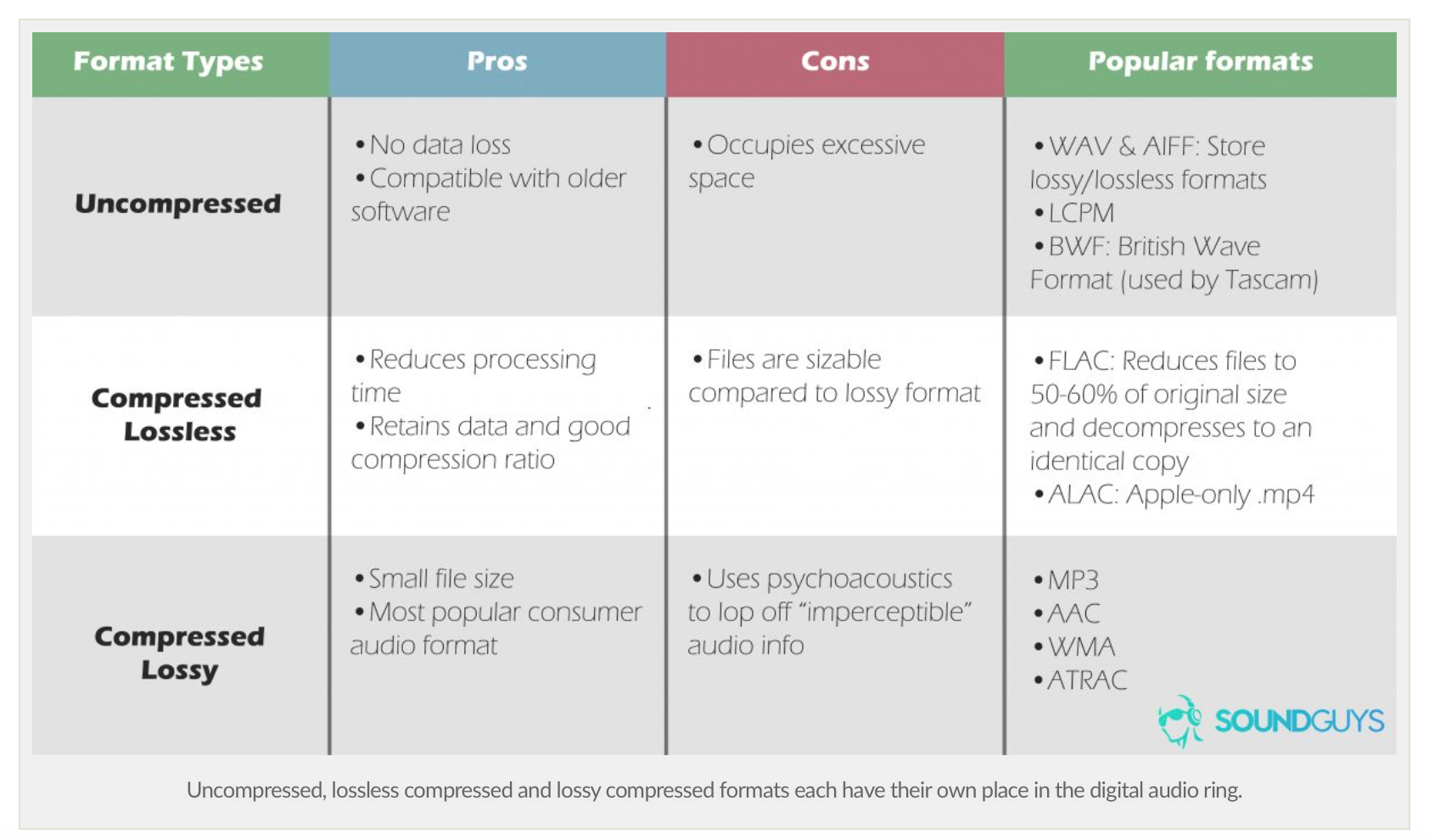
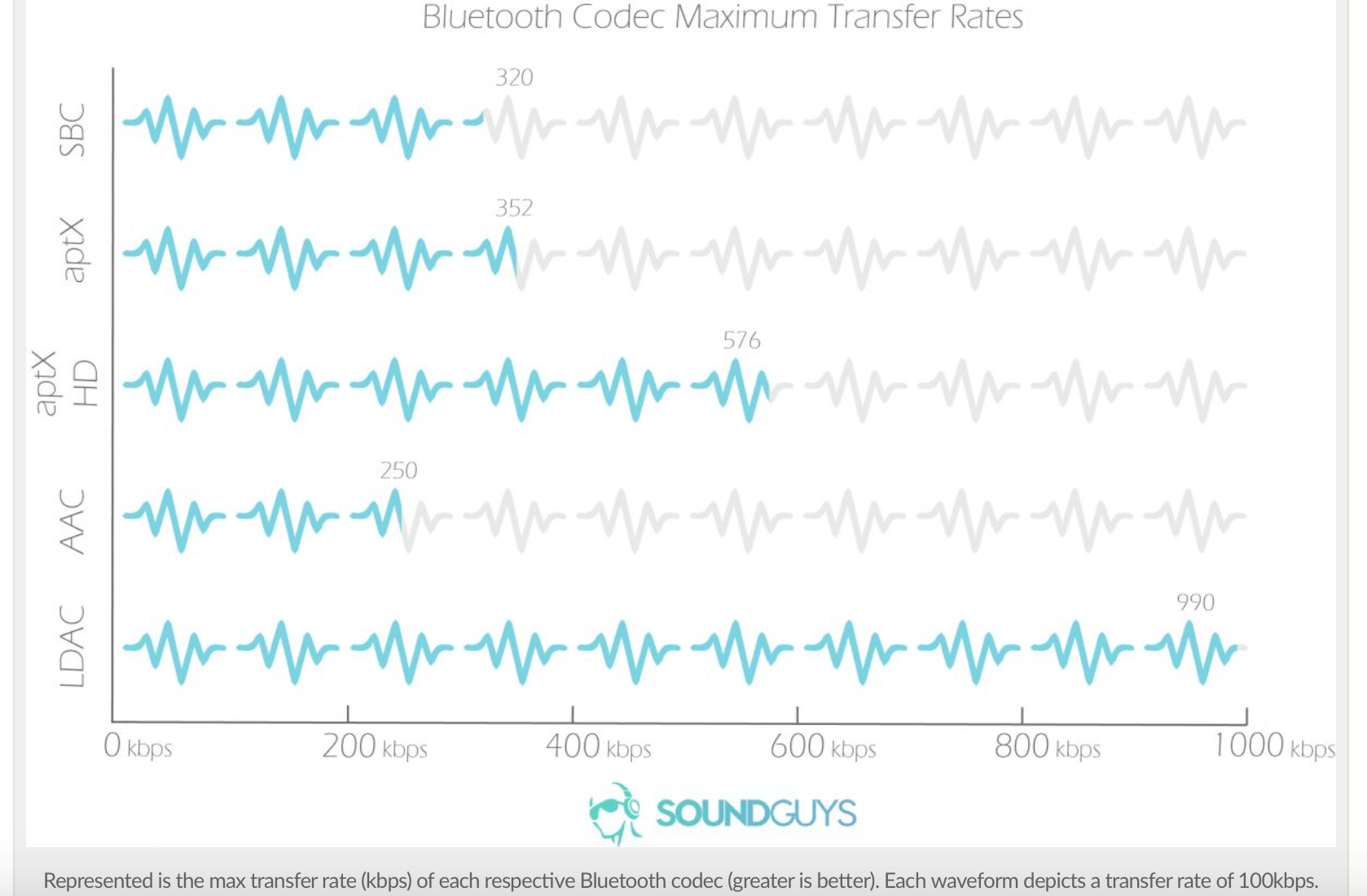
开发BT audio,经常被各种BT music 断音,跳音等等问题而困扰,大部分都是因为codec出问题或是bt受干扰而throughput不够。
针对BT music使用到的codec,这篇文章有做一些总结。Understanding Bluetooth codecs
测试之道
Google认为tester是为了帮助RD提高生产效率的,并不是为了把关什么软件质量,只有RD才能真正把关质量。
由于公司是IC 设计公司,所有的软件定义都是为IC 服务,软件开发时程也是紧跟硬件的时程。SW RD的产出有很大一部分时候需要靠QA来帮忙做测试抓问题,而不是RD自己把code写的铜墙铁壁,没有漏洞。。反过来说,对RD也是一个很大的考验,如何在短时间内高质量完成自己的部分,而且不over design。
通信相关的文章收集
IQ调制:http://blog.chinaaet.com/molf/p/29748
通信介绍:https://zhuanlan.zhihu.com/p/23612006
https://www.cnblogs.com/shaoyou/p/4822222.html
https://en.wikipedia.org/wiki/File:Fourier_series_and_transform.gif
https://en.wikipedia.org/wiki/File:Fourier_series_square_wave_circles_animation.gif
https://en.wikipedia.org/wiki/File:Fourier_series_sawtooth_wave_circles_animation.gif